Tech Interview
A site for technical interview questions, brain teasers, puzzles, quizzles (whatever the heck those are) and other things that make you think!
Category: regular
-
-
Chessboard
Posted at 11:35 am , on April 16, 2010
problem: using 31 dominoes, where one domino covers exactly two squares, can you cover all the empty squares on this chessboard (which has 62 spaces). if so, how? if not, why?
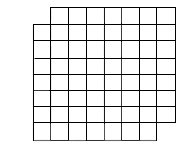
Solution
i think everyone’s first inclination is to try and figure out how it is possible. then again, if you’ve heard a bunch of these questions before, you usually know that if the question says “if not, why?” or “prove whether its possible or impossible”, you can infer that it is not possible (otherwise, the question usually just asks for the solution).
-
Easy River Crossing
Posted at 11:33 am , on April 16, 2010
Three cannibals and three anthropologists have to cross a river. the boat they have is only big enough for two people. if at any point in time there are more cannibals on one side of the river than anthropologists, the cannibals will eat them. what plan can the anthropologists use for crossing the river so they don’t get eaten?
-
Shapes
Posted at 11:29 am , on April 16, 2010
Part I: draw a square. divide it into four identical squares. remove the bottom left hand square. now divide the resulting shape into four identical shapes.
Part II: draw an equilateral triangle (all sides same length). divide it into four identical shapes. remove the bottom left hand shape. now divide the resulting shape into four identical shapes.
-
Webloggers
Posted at 11:25 am , on April 16, 2010
Five webloggers – joshua Allen, meg Hourihan, jason Kottke, robert Scoble, and joel Spolsky – were competing for karma points on the major search engines: google, yahoo, altavista, lycos, and msn. karma was distributed on a five point scale. the most popular weblog received 5 points, and the least popular received 1 point. for each search engine, no two webloggers received the same number of points. overall scores were determined by adding up the individual scores from each search engine.
-
Hard River Crossing
Posted at 12:47 pm , on April 15, 2010
a disfunctional family has to cross the river. on one side of the river are a mom and 2 daughters, dad and 2 sons, the maid and the dog. there is a boat only big enough to hold 2 people (counting the dog as 1 person). only the adults are capable of operating the boat. everyone has to get to the other side, without anything bad happening.
-
Classic Weighing
Posted at 12:44 pm , on April 15, 2010
this is a classic problem which i have heard many times before. this is the “harder” of the two problems, since in this one, you do not know if the invalid item weighs more or less than the others.
solving it is only half the battle. writing up a solution that anyone including your grandma could understand, is very hard.
-
Monty Hall Problem
Posted at 12:40 pm , on April 15, 2010
Another well known problem in probability is the Monty Hall problem.
You are presented with three doors (door 1, door 2, door 3). one door has a million dollars behind it. the other two have goats behind them. You do not know ahead of time what is behind any of the doors.
-
Gold Chain
Posted at 12:51 pm , on April 14, 2010
A man has a gold chain with 7 links. he needs the service of a laborer for 7 days at a fee of one gold link per day. however, each day of work needs to be paid for separately. in other words, the worker must be paid each day after working and if the laborer is ever overpaid he will quit with the extra money. also he will never allow himself to be owed a link.
-
Surgeons
Posted at 12:49 pm , on April 14, 2010
A one armed surgeon with a hand wound needs to operate on three patients. the surgeon only has two gloves. how can he operate on the three patients in turn without risking exchange of fluids? (remember he only has one arm so he only needs to wear one glove at a time.)
-
Clock
Posted at 12:46 pm , on April 14, 2010
Part I: what is the angle between the minute hand and the hour hand at 3:15 on an analog clock? no, its not 0.
Part II: how often does the minute hand pass the hour hand on an analog clock?
Solution
part I: 12 hours on the clock make 360 deg. so one hour is 30 deg. the hour hand will be directly on the 3 when the minute hand is at 12 (3:00). after 15 minutes or 1/4 of an hour, the hour hand will be 1/4 * 30 deg = 7.5 deg. away from the minute hand.
-